
無差別曲線と予算制約線
経済学は数学的要素の強い学問です。消費者理論における効用最大化とは、ある一定の制約条件(予算制約)下における効用の極大値(微分してゼロ)を求める数学と置き換えることもできます。
人間は効用を最大化したいと思って行動します。しかし、現実的にはあらゆる制約があり、なんでも自由に行動できるというわけではありません。
消費者理論の効用最大化問題では、所得という予算が制約条件となります。
経済学では、この制約条件を予算制約式、グラフでは予算制約線で表します。また、無差別曲線や予算制約線は序数的分析ですので、通常は2財モデル(2つの商品)で分析します。
消費者理論の一般均衡分析では、無差別曲線で人の満足度を表現します。無差別曲線とは山の等高線のイメージです。地図帳などで見かけるあの同心円の線です。
人は、まずゼロからスタートします。最適な労働を行うことで得た予算で、人生という山をもっとも高い位置まで登れるルートで登っていくイメージです。
無差別曲線は各自の人生という山の等高線ですので、人によって形や傾斜が異なります。
また、予算制約線は所得だけではなく、購入しようと思っている商品の価格の変化によっても、登れる位置の変化をもたらします。
まとめると、人の幸せの形(無差別曲線)は人の数だけ無数にあり、また、世の中にある無数のアイテムや人生に関わるあらゆるものを、現在の制約条件(予算制約線)のなかでいかに最適に組み合わせるかを考えることに他なりません。
2財モデル~代替材or補完財
2つの商品を同時に分析する2財モデルは、ミクロ経済学の主流です。
世の中から2つの商品をピックアップして分析する場合、大きくは次の2つに大別できます。
①代替材モデル・・・2財モデルは、経済学ではほとんど場合、代替財モデルです。代替財とは、コーヒーと紅茶、ビールとハイボール、うどんとそばのように、どちらにしますか(or)というイメージです。ランチのあと、「食後のドリンクは、コーヒーになさいますか、それとも紅茶になさいますか」といった感じですね。お互いが代わりになることができる2財を、そのままなのですが代替財と呼びます。
②補完財モデル・・・2財モデルのうち、ふたつをセットで利用するものを補完財と呼びます。代替財が「or」なら、補完財は「and」のイメージです。例としては、コーヒーと砂糖、右の靴と左の靴、右の手袋と左の手袋などです。補完財という名の通り、常に組み合わせて一緒に消費するので、ふたつ揃わないと効用は上がりません。ランチのあとに、「食後はコーヒーをお飲みになりますか、それとも砂糖をかじられますか」ではなく、「コーヒーに砂糖やミルクはいくつ必要でしょうか」といった聞き方が通常ですよね。
効用最大化とは
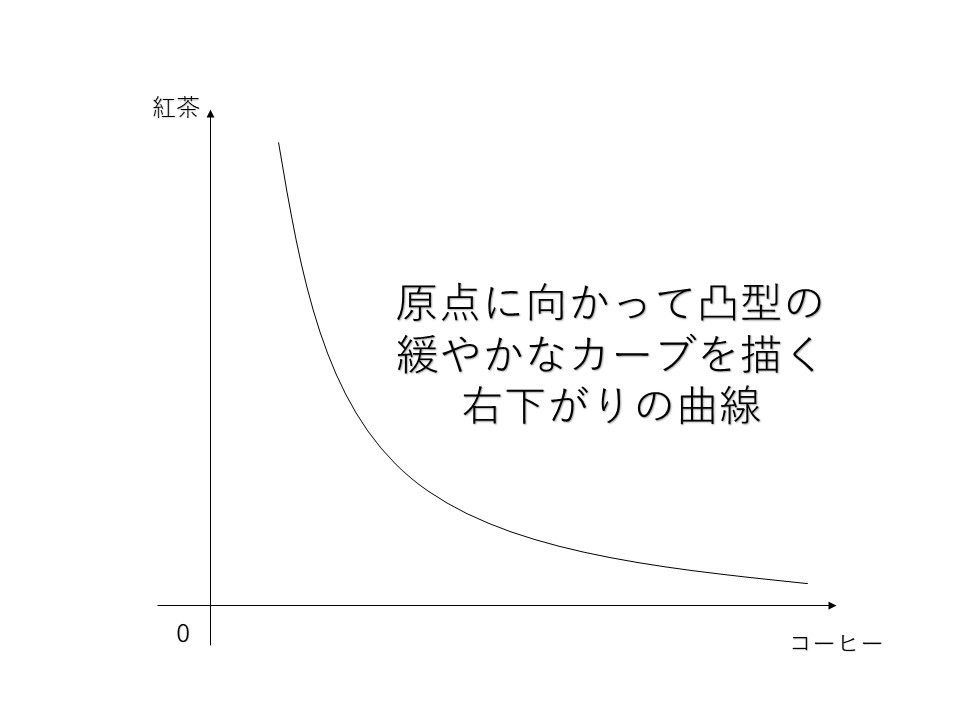
代替財の無差別曲線は、以下のように表されます。表中にも記しているように、原点に向かって凸型の緩やかなカーブを描く右下がりの曲線となります。
無差別曲線は人生における山の等高線なので、一本の線上はどこをとっても同じ効用水準ということになります。
人はある一定の制約条件のなかで、効用の最大化を目指します。経済学における制約条件とは予算に他なりません。
最適なワークライフバランスを実現していることを前提に、稼いだお金で好きなものを組み合わせて買うイメージです。
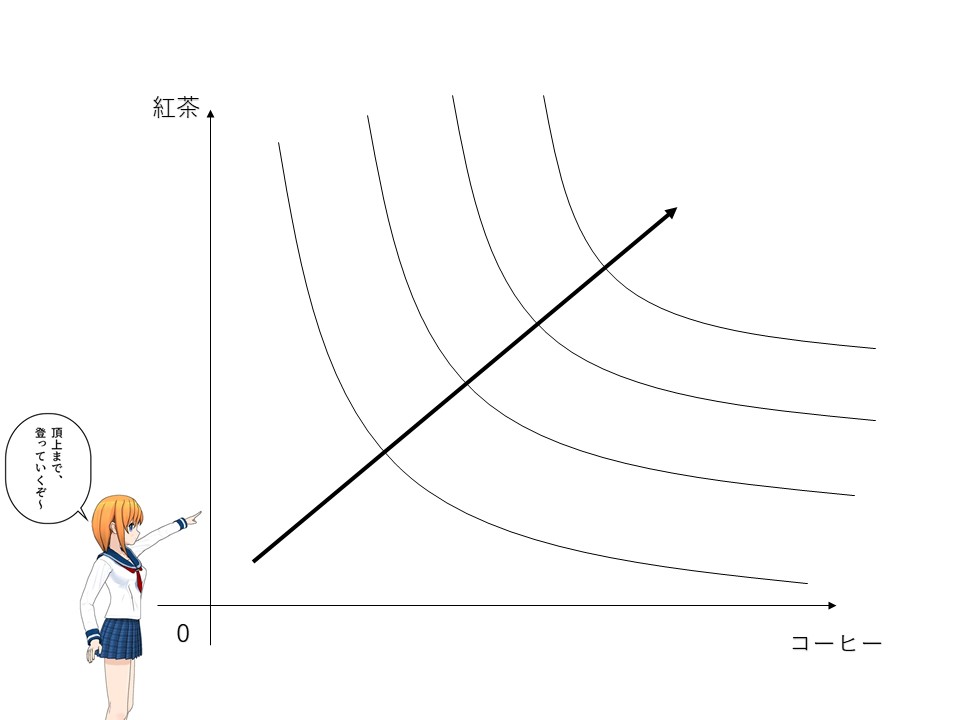
世の中の経済は、人間の限りない欲求をエネルギーとして回っています。人は、好きなものをより多く手に入れたいと願い、行動しています。したがって、コーヒーだろうが、紅茶だろうが、好きなものであれば手に入れれば入れるほど幸せを感じることができます。上図のように右上(右にいけばコーヒー、上にいけば紅茶をより多く手に入れることを意味します)にいけばいくほど、より多くのものを手に入れていることになりますので、満足(効用)も上昇します。
人生を山に例えれば、何も持っていない状態(原点)から出発し、一歩ずつ右上にあるであろう頂上を目指して登っていく感じです。自分がいまどこまで登れたか、その到達度を表しているのが、人生という山の等高線=無差別曲線ということになります。
したがって、右上にある無差別曲線ほど、より高い効用水準を表していることになります。
予算制約線とは
お金が無限にあれば、好きなものを好きなだけ買って、毎日、遊んで暮らせばよいのですが、ほとんどの人はそういうわけにはいきません。最適なワークライフバランスで働いて、得た所得を基準に消費活動を行います。
予算制約線とは、消費者一人ひとりの現時点における制約条件をグラフ化したものです。
具体例を挙げてみます。
いま、お財布の中に1,000円あります。コーヒーは200円、紅茶は250円のときの予算制約線を描きなさい、と言われたらどうでしょう。
1,000円ありますから、コーヒーだけなら5杯、紅茶だけなら4杯購入できますね。これをグラフに表せば、下図のようになります。


コメント